- Home
- Geometry
- Angles Worksheets
- Pair of Angles
Categories
- Algebra
- Multiplying Polynomials
- Subtracting Polynomials
- Adding Polynomials Worksheets
- Classifying Polynomials
- Proportion Worksheets
- Trigonometric Charts
- Quadrants Worksheets
- Roots of Quadratic Equation
- Solving Quadratic Equation Worksheets
- Multi Step Equation Worksheets
- Two Step Equation Worksheets
- One Step Equation Worksheets
- Identifying Polynomials Worksheets
- Evaluate Algebraic Identities
- Algebraic Expressions
- Scientific Notation
- Order of Operations
- Simplifying Algebraic Expressions
- Graphing Lines
- Point Slope Form Worksheets
- Two Point Form Worksheets
- Ratio Worksheets
- Two Intercept Form
- Data Handling
- English Worksheets
- Geometry
- Factors and Multiples
- Measuring Angles
- Types of Angles
- Pair of Angles
- Naming Angles Worksheets
- Composing and Decomposing Shapes
- Angles in Triangles
- Triangle Inequality Theorem
- Medians and Centroid of a triangle
- Pythagorean Theorem
- Perimeter of Triangles
- Types of Triangles
- Area of Triangles
- Circumference of Circles
- Area of Circles
- Perimeter of Rectangles
- Area of Rectangle
- Identifying Rectangles
- Perimeter of Squares
- Area of Squares
- Identifying Quadrilaterals
- Area of Quadrilaterals
- Perimeter of Quadrilaterals
- Slope Worksheets
- Distance Worksheets
- Midpoint Formula
- Kite Worksheets
- Parallelogram Worksheets
- Lines, Rays, Line Segments and Planes
- Symmetry Worksheets
- 3D Shapes Worksheets
- 2D Shapes Worksheets
- Complementary and Supplementary Angles
- Kids Corner
- Veteran’s Day Worksheets
- Valentine’s Day Worksheets
- Thanksgiving Day Worksheets
- Labor Day Worksheets
- Saint Patrick’s Day Worksheets
- Memorial Day Worksheets
- Martin Luther King Worksheets
- Halloween Worksheets
- Columbus Day Worksheets
- New Year Worksheets
- Christmas Worksheets
- Easter Worksheets
- Matching Activity
- Connecting Dots
- Tracing and Coloring
- Coloring Activity
- Cartoon Coloring
- Number Names Charts
- Number Charts
- Standard Charts
- Alphabet
- Measurement
- Numbers & Operations
- Polynomials – Box method
- Dividing Polynomials Worksheets
- Place value for Decimals
- 6-Digit Place Value Worksheets
- 5-Digit Place Value Worksheets
- 4 Digit Place Value Worksheets
- 3-Digit Place Value Worksheets
- 2 Digit Place Value Worksheets
- Patterns Worksheets
- Types of fractions
- Multiplying and Dividing fractions
- Comparing and Ordering fractions
- Fraction Subtraction
- Fraction Addition
- Representing fractions
- Exponents Worksheets
- Ordering Numbers
- Estimation of Numbers
- Page Template
- Rounding Numbers
- Cardinal & Ordinal Numbers
- Odd and Even Numbers
- Skip Counting Worksheets
- Roman Numerals Worksheets
- Decimal Subtraction
- Decimal Addition
- Prime and Composite Numbers
- Squares and Cubes of Numbers
- Divisibility Rules Worksheets
- Counting & Cardinality
- Addition Tables
- Word Problems
Pair Of Angles Worksheets
The previous sets of worksheets are on complementary and supplementary pairs of angles.
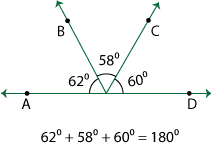
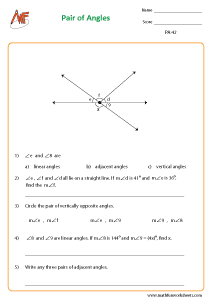
Now, we will learn more pairs of angles for grade 6 to grade 8 like linear, vertically opposite and adjacent angles here. Before you know all these pairs of angles there is another important concept which is called ‘angles on a straight line’. The sum of angles on a straight line is 180 degree. Thus, any number of angles on a straight line amounts to 180 degree.
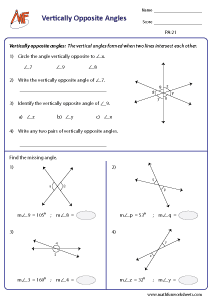
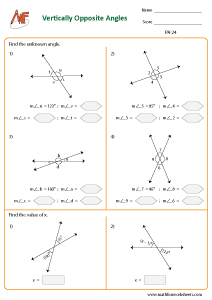
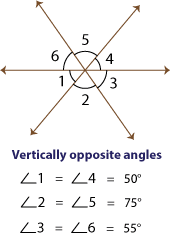
Vertically opposite angles:
Vertical angles or vertically opposite angles are opposite angles formed when two lines intersect each other. Thus, two pairs of opposite angles are formed when two lines intersect. Here, the pair of opposite angles are equal. Refer the figure given below for clear understanding.
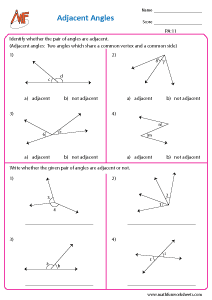
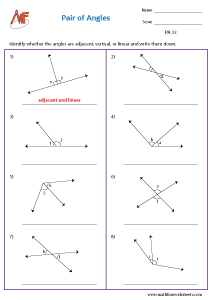
Adjacent angles:
Two angles are said to be adjacent, if they have a common vertex and a common arm. The angles should not overlap which means the other arms are lying on the opposite side of the common arm.
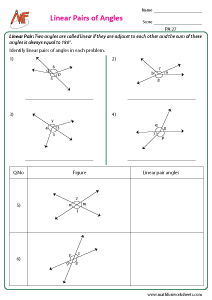
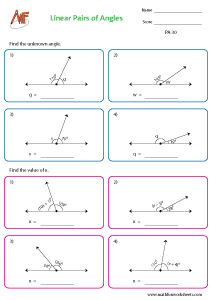
Linear pair of angles:
Two adjacent angles whose sum is always 180 degree form a linear pair. They can also be called as supplementary angles.
All you need to do now is to just print all these worksheets and work on them. Only when you are thorough with these concepts, you can understand corresponding and alternate angles. Also, these pairs of angle are very important to find the missing measures of angles in interior and exterior angle concept.
Identify and differentiate the different pairs of angles, find the missing measure of angles, solve equations and word problems in these free pintables. Examples are shown wherever necessary.
RELATED GEOMETRY TOPICS : 2D Shapes, 3D Shapes, Lines rays line segments and planes, Composing and Decomposing shapes
Pair of Angles Worksheets
-
Check if the pair of angles are adjacent
Check if the pair of angles are adjacent
-
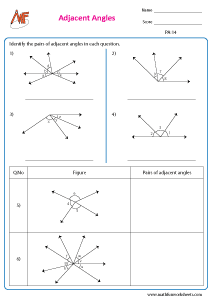
Identify the pair of adjacent angles
Identify the pair of adjacent angles
-
Adjacent angles - mixed review
Adjacent angles - mixed review
-
Find the missing value - vertically opposite angles
Find the missing value - vertically opposite angles
-
Find the unknown angle - vertically opposite angles
Find the unknown angle - vertically opposite angles
-
Identify linear pair of angles
Identify linear pair of angles
-
Find the unknown angle - Linear pair of angles
Find the unknown angle - Linear pair of angles
-
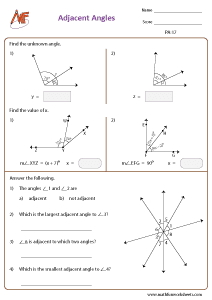
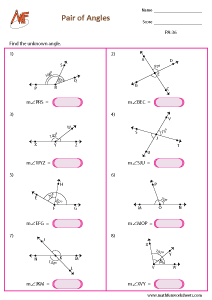
Find the unknown angle - pair of angles
Find the unknown angle - pair of angles
-
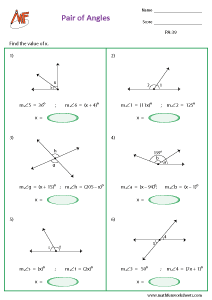
Find the value of x - pair of angles
Find the value of x - pair of angles
